Sums of Distances
University of Liverpool Maths Club, 23 February 2002
Peter Giblin
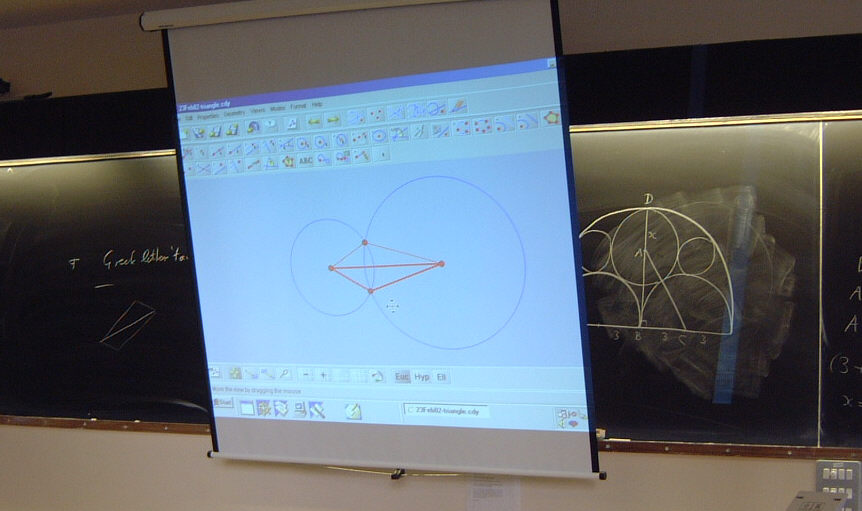
First, look at constructing a triangle \(ABC\) with sides of three
given lengths \(a\), \(b\), \(c\). We lay out the line \(BC\) along the horizontal say, and
draw circles centre \(A\), radius \(b\), and centre \(B\), radius \(a\).
See the applet: 23Feb02-triangle-lab
Notice that the triangle \(ABC\) is sometimes above the line \(BC\) and sometimes underneath it! There is an alternative, \(ABD\), with the same side lengths as \(ABC\).
Clicking on a circle it can be changed in radius. The points \(C\) and \(D\) disappear if the circles are changed so as not to meet. This gives inequalities for the lengths of the sides of the triangle, such as \(a + b > c\), or \(a + b = c\) for a 'flat' triangle.
These ideas are then applied to four points \(A, B, C, D\) in the plane: what is the best place to site a road junction \(F\) so that \(AF + BF + CF + DF\) is as small as possible? It turns out that if the quadrilateral \(ABCD\) is 'convex' (all interior angles less than 180 degrees) the best site is at the intersection of the diagonals of the quadrilateral.
You can experiment with this applet. If you try putting \(D\) inside the triangle \(ABC\), the result is quite different....
You can also find out how to make a five-road connection between \(A, B, C, D\) in the case of a rectangle. Try 23Feb02-rect.html Where do you think the points inside should be so that the sum of the blue lines is as short as possible?
The final section is on the harder problem of three given points \(A, B, C\); we look for a point \(F\) so that \(AF + BF + CF\) is as small as possible.The applets: steiner3.html steiner3a.html
In the latter, try to move \(F\) so that the brown line is along the same line as the yellow and black lines; then \(F\) will be in the best position. The angles around \(F\) are then all 60 degrees or 120 degrees. The applet steiner5.html shows a construction for a point \(F\) with angles all round of 60 degrees, \(F\) being the intersection of the three thin red lines in the figure. The proof of this is sketched in the notes for the presentation.